Benford's Law
Warning: Đây không phải 1 vấn đề về tech =))
Hãy nghĩ tới 1 tập hợp các con số trong tự nhiên. Ví dụ: Chiều cao của các ngôi nhà trên thế giới, chiều dài của nột con sông, lợi nhuận của 1 công ty, kết quả trận bóng chày, tỉ lệ tử vong, giá cổ phiếu, địa chỉ nhà, hoá đơn điện,… Những con số này có tuân theo quy luật gì không?
Nghe thì có vẻ là không, vì những con số này khá là “tự nhiên” =)) Tuy nhiên, năm 1938, nhà vật lý Frank Benford đã kiểm chứng dữ liệu trên 20 lĩnh vực khác nhau, và phát hiện được 1 quy luật:
Các con số (hệ thập phân) của một thống kê trong tự nhiên có một tính chất kì lạ là: Chữ số đầu tiên của các kết quả có một phân bố không đồng đều và tuân thủ theo quy luật giảm dần, số 1 có xác suất xuất hiện khoảng 30%, số 2 khoảng 17.6%, … số 9 khoảng 4.5%
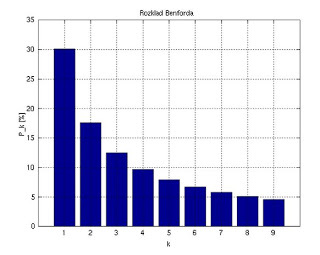
Nếu các số từ 1 đến 9 được phân bố đồng đều thì mỗi số phải xuất hiện khoảng 11.1% (= 1⁄9), nhưng qua việc đo kiểm, thực tế xác suất xuất hiện của chúng chênh nhau khá lớn =)) Khá thú vị đúng không =))
Luật này còn được biết đến với cái tên khác như luật Newcomb-Benford, luật số bất thường, hay luật chữ số thứ nhất.
Các nhà nghiên cứu cũng đã dùng luật Benford để tìm ra các số liệu giả mạo trong kê khai thuế và dữ liệu tài chính, hoặc kiểm tra sự bất quy tắc trong các cuộc thử nghiệm thuốc hay xác thực các mô hình biểu đồ dữ liệu, …